- Research
- Open access
- Published:
Sample size and power estimation for studies with health related quality of life outcomes: a comparison of four methods using the SF-36
Health and Quality of Life Outcomes volume 2, Article number: 26 (2004)
Abstract
We describe and compare four different methods for estimating sample size and power, when the primary outcome of the study is a Health Related Quality of Life (HRQoL) measure. These methods are: 1. assuming a Normal distribution and comparing two means; 2. using a non-parametric method; 3. Whitehead's method based on the proportional odds model; 4. the bootstrap. We illustrate the various methods, using data from the SF-36. For simplicity this paper deals with studies designed to compare the effectiveness (or superiority) of a new treatment compared to a standard treatment at a single point in time. The results show that if the HRQoL outcome has a limited number of discrete values (< 7) and/or the expected proportion of cases at the boundaries is high (scoring 0 or 100), then we would recommend using Whitehead's method (Method 3). Alternatively, if the HRQoL outcome has a large number of distinct values and the proportion at the boundaries is low, then we would recommend using Method 1. If a pilot or historical dataset is readily available (to estimate the shape of the distribution) then bootstrap simulation (Method 4) based on this data will provide a more accurate and reliable sample size estimate than conventional methods (Methods 1, 2, or 3). In the absence of a reliable pilot set, bootstrapping is not appropriate and conventional methods of sample size estimation or simulation will need to be used. Fortunately, with the increasing use of HRQoL outcomes in research, historical datasets are becoming more readily available. Strictly speaking, our results and conclusions only apply to the SF-36 outcome measure. Further empirical work is required to see whether these results hold true for other HRQoL outcomes. However, the SF-36 has many features in common with other HRQoL outcomes: multi-dimensional, ordinal or discrete response categories with upper and lower bounds, and skewed distributions, so therefore, we believe these results and conclusions using the SF-36 will be appropriate for other HRQoL measures.
Introduction
Health Related Quality of Life (HRQoL) measures are becoming more frequently used in clinical trials as primary endpoints. Investigators are now asking statisticians for advice on how to plan (e.g. estimate sample size) and analyse studies using HRQoL measures.
Sample size calculations are now mandatory for many research protocols and are required to justify the size of clinical trials in papers before they will be accepted by journals [1]. Thus, when an investigator is designing a study to compare the outcomes of an intervention, an essential step is the calculation of sample sizes that will allow a reasonable chance (power) of detecting a predetermined difference (effect size) in the outcome variable, at a given level of statistical significance. Sample size is critically dependent on the purpose of the study, the outcome measure and how it is summarised, the proposed effect size and the method of calculating the test statistic [2]. For simplicity in this paper we will assume that we are interested in comparing the effectiveness (or superiority) of a new treatment compared to a standard treatment at a single point in time.
HRQoL measures such as the Short Form (SF)-36, Nottingham Health Profile (NHP) and European Organisation for Research and Treatment of Cancer (EORTC) QLQ-C30 are described in Fayers and Machin [3] and are usually measured on an ordered categorical (ordinal) scale. This means that responses to individual questions are usually classified into a small number of response categories, which can be ordered, for example, poor, moderate and good. In planning and analysis, the responses are often analysed by assigning equally spaced numerical scores to the ordinal categories (e.g. 0 = 'poor', 1 = 'moderate' and 2 = 'good') and the scores across similar questions are then summed to generate a HRQoL measurement. These 'summated scores' are usually treated as if they were from a continuous distribution and were Normally distributed. We will also assume that there exists an underlying continuous latent variable that measures HRQoL (although not necessarily Normally distributed), and that the actual measured outcomes are ordered categories that reflect contiguous intervals along this continuum.
However, this ordinal scaling of HRQoL measures may lead to several problems in determining sample size and analysing the data [4, 5]. The advantages in being able to treat HRQoL scales as continuous and Normally distributed are simplicity in sample size estimation and statistical analysis. Therefore, it is important to examine such simplifying assumptions for different instruments and their scales. Since HRQoL outcome measures may not meet the distributional requirements (usually that the data have a Normal distribution) of parametric methods of sample size estimation and analysis, conventional statistical advice would suggest that non-parametric methods be used to analyse HRQoL data [3].
The bootstrap is an important non-parametric method for estimating sample size and analysing data (including hypothesis testing, standard error and confidence interval estimation) [6]. The bootstrap is a data based simulation method for statistical inference, which involves repeatedly drawing random samples from the original data, with replacement. It seeks to mimic, in an appropriate manner, the way the sample is collected from the population in the bootstrap samples from the observed data. The 'with replacement' means that any observation can be sampled more than once. HRQoL outcome measures actually generate data with discrete, bounded and non-standard distributions. So, in theory, computer intensive methods such as the bootstrap that make no distributional assumptions may therefore be more appropriate for estimating sample size and analysing HRQoL data than conventional statistical methods.
Conventional methods of sample size estimation for studies with HRQoL outcomes are extensively discussed in Fayers and Machin [3]. However, they did not use the bootstrap to estimate sample sizes for studies with HRQoL outcomes. As a consequence of this omission, the aim of this paper is to describe and compare four different methods, including the bootstrap for estimating sample size and power when the primary outcome is a HRQoL measure.
To illustrate this, we use some HRQoL data from a randomised controlled trial, the Community Postnatal Support Worker Study (CPSW), which aimed to compare the difference in health status in a group of women who were offered postnatal support (intervention) from a community midwifery support worker compared with a control group of women who were not offered support [7]. The primary outcome (used to estimate sample size for this study) was the general health dimension of the SF-36 at 6 weeks postnatally.
Methods
SF-36 Health Survey
The SF-36 is the most commonly used health status measure in the world today [8]. It originated in the USA [9], but has been validated for use in the UK [10]. It contains 36 questions measuring health across eight different dimensions – physical functioning (PF), role limitation because of physical health (RP), social functioning (SF), vitality (VT), bodily pain (BP), mental health (MH), role limitation because of emotional problems (RE) and general health (GH). Responses to each question within a dimension are combined to generate a score from 0 to 100, where 100 indicates "good health". Thus, the SF-36 generates a profile of HRQoL outcomes, (see Figure 1), on eight dimensions.
Which sample size formulae?
In principle, there are no major differences in planning a study using HRQoL outcomes, such as the SF-36, to those using conventional clinical outcomes. Pocock [11] outlines five key questions regarding sample size:
-
1.
What is the main purpose of the trial?
-
2.
What is the principal measure of patient outcome?
-
3.
How will the data be analysed to detect a treatment difference?
-
4.
What type of results does one anticipate with standard treatment?
-
5.
How small a treatment difference is it important to detect and with what degree of certainty?
Given answers to all of the five questions above, we can then calculate a sample size.
The choice of the sample size formulae strictly depends on the way data will be analysed, which in turn depends on specific characteristics of the data analysed. For this reason this paper is not only a comparison of four methods of sample size calculation, but also the comparison of the power of four different methods of analysis. We describe four methods of sample-size estimation when using the SF-36 in the comparative clinical trials of two treatments (Table 1). The first method (Method 1) assumes the various individual dimensions of the SF-36 are continuous and Normally distributed. The second method (Method 2) assumes the SF-36 dimensions are continuous. The third method (Method 3) assumes the SF-36 is an ordered categorical outcome. The fourth method uses a bootstrap approach.
In this paper the bootstrap has two roles. It is one of the four methods of sample size calculation and consequently analysis but it is also the method used to estimate the power curves presented in the figures. The bootstrap, in the way used in this paper, is a procedure for evaluating the performance of the statistical procedures, including tests. The bootstrap is non parametric in the sense that it evaluates the performance of any test statistic without making assumptions about the form of the distribution. For the methods of sample size estimation, we consider three test statistics, Methods 1, 2 and 3 and evaluate two of them in two ways, one using the usual assumptions (Normality or continuity), and the other by generating bootstrap distributions from the data.
Method 1 Normally distributed continuous data – comparing two means
Suppose we have two independent random samples x1, x2,...,xm and y1, y2,....,yn, of HRQoL data of size m and n respectively. The x's are y's are random samples from continuous HRQoL distributions having cumulative distribution functions (cdfs), Fx and Fy respectively. We will consider situations where the distributions have the same shape, but the locations may differ. Thus if δ denotes the location difference (i.e. mean (y) - mean (x) = δ), then FY(y) = FX(y - δ), for every y. We shall focus on the null hypothesis H0: δ = 0 against the alternative HA: δ ≠ 0. We can test these hypotheses using an appropriate significance test (e.g. t-test). With a Normal distribution under the location shift assumption and with n = m, the necessary sample size to achieve a power of 1-β is given in Table 1.
Method 2 continuous data using non-parametric methods
If the HRQoL outcome data (i.e. the GH dimension of the SF-36) is assumed continuous and plausibly not sampled from a Normal distribution then the most popular (not necessarily the most efficient), non-parametric test for comparing two independent samples is the two-sample Mann-Whitney U (also known as the Wilcoxon rank sum test) [12].
Suppose (as before) we have two independent random samples of x's and y's and we want to test the hypothesis that the two samples have come from the same population against the alternative that the Y observations tend to be larger than the X observations. As a test statistic we can use the Mann-Whitney (MW) statistic U, i.e., U = #(yj > xi), i = 1,...,m; j = 1,...,n, which is a count of the number of times the yjs are greater than the xis. The magnitude of U has a meaning, because U/nm is an estimate of the probability that an observation drawn at random from population Y would exceed an observation drawn at random from population X, i.e. Pr(Y > X).
Noether [13] derived a sample size formula for the MW test (see Table 1), using an effect size pNoether, (i.e. Pr(Y > X)), that makes no assumptions about the distribution of the data (except that it is continuous), and can be used whenever the sampling distribution of the test statistic U can be closely approximated by the Normal distribution, an approximation that is usually quite good except for very small n [14].
Hence to determine the sample size, we have to find the 'effect size' pNoether or the equivalent statistic Pr(Y > X). There are several ways of estimating pNoether, under various assumptions, one non-parametric possibility is pNoether = U/nm. Unfortunately, this can only be estimated after we have collected the data and calculated the U statistic or by computer simulation (as we shall see later). If we assume that X ~ N(μ
X, σ2
X) and Y ~ N(μ
Y, σ2
Y) then a parametric estimate of Pr(Y > X) using the sample estimates of the mean and variance ( ) is given by [15]:
) is given by [15]:

where Φ is the Normal cumulative distribution function.
If we assume the SF-36 is Normally distributed then equation 1 allows the calculation of two comparable 'effect sizes' pNoether and Δ Normal thus enabling the two methods of sample size estimation to be directly contrasted. If the SF-36 is not Normally distributed then we cannot use equation 1 to calculate comparable effect sizes and must rely on the empirical estimates of pNoether = U/nm calculated post hoc from the data. Alternatively, under the location shift assumption, we can use bootstrap methods to estimate pNoether.
Method 3 – Ordinal data and Whitehead's Odds Ratio
Whitehead [16] has derived a method for estimating sample sizes for ordinal data and suggested the odds ratio (OROrdinal), which is the odds of a subject being in a given category or lower in one group compared with the odds in the other group, as an effect size. To use Whitehead's formulae the proportion of subjects in each scale category for one of the groups must also be specified.
Suppose there are two groups T and C and the HRQoL outcome measure of interest Y has k ordered categories yi denoted by i = 1,2,...,k. Let π iT be the probability of a randomly chosen subject being in category i in Group T and γ iT be the expected cumulative probability of being in category i or less in Group T (i.e. γ iT = Pr(Y ≤ yi)). For category i, where i takes values from 1 to k-1, the ORi is given in Table 1.
The assumption of proportional odds specifies that the ORi will be the same for all categories from i = 1 to k-1. As the derivation of the sample size formulae and analysis of data is based on the Mann-Whitney U test, Whitehead's method can be regarded as a 'non-parametric' approach, although it still relies on the assumption of a constant OR for the data. Whitehead's method also assumes a relatively small log odds ratio and a large sample size, which will often be the case in HRQoL studies where dramatic effects are unlikely [4]. Table 1 gives the number of subjects per group nOrdinal for a two-sided significance level α and power 1-β.
Whitehead's [16] method for sample determination is derived from the proportional odds model. The proportional odds model is equivalent to the MW test when there is only a 0/1 (or group) variable in the regression [17]. The advantage of the proportional odds model, over the MW test is that it allows the estimation of confidence intervals for the treatment group effect and for the adjustment of the HRQoL outcome for other covariates.
If the number of categories is large, it is difficult to postulate the proportion of subjects who would fall in a given category. Whitehead [16] points out that there is little increase in power (and hence saving in the number of subjects recruited) to be gained by increasing the number of categories beyond five. An even distribution of subjects within categories leads to the greatest efficiency.
Shepstone [18] demonstrates how the three seemingly different effect size measures Δ Normal, OROrdinal and pNoether, which are all numerical expressions of treatment efficacy can be combined into a common scale. If Y and X are the values of an outcome (higher values more preferable) for randomly selected individuals from the Treatment and Control groups respectively, then AYX = Pr(Y > X), i.e. the probability that the Treatment patient has an outcome preferable to that of the Control patient, is equivalent to the effect size statistic pNoether. If we let AXY = Pr(X > Y), i.e. the probability that a random individual from group 2 (Control) has a better outcome than a random individual from group 1 (Treatment), then
λ = A YX - A XY = Pr(Y >X) - Pr(X >Y) (2)
and

Shepstone [18] shows that for ordinal and continuous outcomes A
YX
- A
XY
= λ and A
YX
/ A
XY
= θ are equivalent to the Absolute Risk Reduction (ARR) and OR for binary outcomes. AXY and AYX, or their equivalent statistics Pr(X > Y) and Pr(Y > X) can be calculated by either a parametric approach for continuous outcomes (Equation 1) via a theoretical distribution (e.g. Normal) or a non-parametric approach without any distributional assumptions via the Mann-Whitney U statistic. (Since AXY and AYX can be estimated by  and
and  where UXY and UYX are the values of the Mann-Whitney U statistics).
where UXY and UYX are the values of the Mann-Whitney U statistics).
If the outcomes are continuous and/or can be fully ranked and there are no ties in the data then Pr(X = Y) = 0 and λ = AYX - AXY = Pr(Y > X) - Pr(X > Y) and θ = AYX/AXY = Pr(Y > X)/Pr(X > Y) can be estimated exactly. Conversely, if there are a large number of ties in the data, i.e. xi = yi, (which is likely for HRQoL outcomes, with their discrete response categories) then Pr(X = Y) > 0. In this case any pairs for which xi = yi, contribute 1/2 a unit to both UYX and UXY. Hence the two A statistics AYX and AXY can only be estimated approximately and thus the approximate estimates of θ and λ in the case of ties will be denoted by θ' and λ' respectively.
Method 4 – Computer simulation – the bootstrap
Methods 1 and 2 assume the HRQoL outcome is continuous and the simple location shift model is appropriate. Here this would imply that, on a certain scale, the difference in effect of the intervention compared to the control is constant or, at least that the intervention shifts the distribution of the HRQoL scores under the control to the right (or to the left if the intervention is harmful) but keeping its shape. However, the boundedness of the SF-36 outcomes renders this location shift assumption questionable, especially if the proportion of cases the upper limit is high. Therefore, we used bootstrap methods to compare the power of the t-test and MW test with allowance for ties for detecting a shift in location using three dimensions of the SF-36 (GH, RP and V) as outcomes [14, 19, 20]. These three dimensions illustrate the different distributions of HRQoL outcomes that are likely to occur in practice.
Suppose (as before) we have two independent random samples of x's and y's from continuous distributions having cdfs, Fx and Fy respectively. Again we will consider situations where the distributions have the same shape, but the locations may differ; i.e. mean (y) - mean (x) = δ. If we focus on the null hypothesis H0: δ = 0 against the alternative HA: δ ≠ 0, then we can test this hypothesis using an appropriate significance test (i.e. t-test, Mann-Whitney or proportional odds model). However, we did not evaluate the proportional odds model as part of the bootstrap. This was because the proportional odds model is equivalent to the MW test when there is only a 0/1 variable in the regression, and the p-values from the MW test and the significance of the regression coefficient for the group variable are indentical [17].
The bootstrap strategy is to use pilot data to a provide a non-parametric estimate

of F and to use a simulation method for finding the power of the test associated with any specified sample size n if the data follow the estimated distribution functions under the null and alternative hypotheses. If we denote the distribution function estimate by 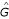 , under the alternative hypothesis δ, we can estimate the approximate power,
, under the alternative hypothesis δ, we can estimate the approximate power, 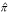 (G, δ, α, n) by the following computer simulation procedure [14, 19, 20].
(G, δ, α, n) by the following computer simulation procedure [14, 19, 20].
Algorithm 1
Power and sample size estimation using the bootstrap
-
1.
Draw a random sample with replacement of size 2 n from F. The first n observations in the sample form a simulated sample of x's, denoted by x1*,...,xn*, with estimated cdf
 *. Then δ is added to each of the other n observations in the sample to form the simulated sample of y's, denoted by y1*,...,yn*, with estimated cdf
*. Then δ is added to each of the other n observations in the sample to form the simulated sample of y's, denoted by y1*,...,yn*, with estimated cdf 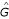 *. (The y*'s and x*'s have been generated from the same distribution except that the distribution of the y*'s is shifted δ units to the right.)
*. (The y*'s and x*'s have been generated from the same distribution except that the distribution of the y*'s is shifted δ units to the right.) -
2.
The test statistic, Mann-Whitney or t-test, is calculated for the x*'s and y*'s, yielding t(x*, y*). If t(x*, y*) ≥ T1-α/2, (where T1-α/2is the critical value of the test statistic) a success is recorded; otherwise a failure is recorded.
-
3.
Steps 1 and 2 are repeated B times. The estimated power of the test,
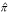
(G, δ α, n), is approximated by the proportion of successes among the B repetitions. (In all cases discussed in this paper, B = 10,000).
The bootstrap procedure described in Algorithm 1 assumes a simple location shift model. For bounded HRQoL outcomes the procedure is in principle the same but more imagination is needed to specify the effect of the new treatment in comparison with the control treatment. Under the simple location shift model, individual improvement of δ points in HRQoL is assumed: for bounded HRQoL outcome scores we have to assume an effect δ 1 (x) such that x + δ (x) remains in the interval determined by the lower and upper boundary of the HRQoL outcome. (In the case of the SF-36 GH dimension between 0 and 100). One function is to assume a constant treatment effect whenever possible. We assumed a constant additional treatment effect of 5 points, until a GH score of 95: patients with a GH score of 95 or more were truncated at 100.
The software Resampling Stats was used for implementing Algorithm 1 [21]. The bootstrap computer simulation procedure involved using SF-36 data from a general population survey based on 487 women aged 16–74 as the pilot dataset (Figure 1) [10].
Results
Sample size estimation – Method 1
When planning the CPSW study we went through Pocock's [11] five key questions regarding sample size.
What is the main purpose of the trial?
To assess whether additional postnatal support by trained Community Postnatal Support Workers could have a positive effect on the mother's general health.
What is the principal measure of patient outcome?
The primary outcome was the SF-36 general health perception (GH) dimension at six weeks postnatally.
How will the data be analysed to detect a treatment difference?
We believed that the mean difference in GH scores between the two groups was an appropriate comparative summary measure and that a two-independent samples t-test would be used to analyse the data.
What type of results does one anticipate with standard treatment?
Unfortunately no information was available from previous studies of new mothers to calculate a sample size based on the GH dimension of the SF-36. Therefore as the CPSW study was only going to involve women of childbearing age we estimated the standard deviation of the GH outcome from a previous survey of the Sheffield general population using (n = 487) females aged 16 to 45 (Figure 1g). This gave us an estimated SD of 20 [10].
How small a treatment difference is it important to detect and with what degree of certainty?
Using the GH dimension of the SF-36, a five-point difference is the smallest score change achievable by an individual and considered as "clinically and socially relevant" [22].
Using Method 1, assuming a standard deviation σ of 20 and that a location shift or mean difference (μ ET - μ EC) of 5 or more points between the two groups is clinically and practically relevant, gives a standardised effect size, Δ Normal, of 0.25. Using this standardised effect size with a two-sided 5% significance level and 80% power gives the estimated required number of subjects per group as 253.
Sample size estimation – Method 2
Suppose we believe the GH dimension to be continuous, but not Normally distributed and are intending to compare GH scores in the two groups with a Mann-Whitney U test (with allowances for ties). Therefore, Noether's method will be appropriate. As before if we assume a mean difference of 5 and a standard deviation of 20 for the GH dimension of the SF-36, then using equation 1 leads to an parametric estimate of the effect size pNoether = Pr(Y > X) of 0.57 and consequently Pr(X > Y) of 0.43. Substituting pNoether = 0.57 in the formula for Method 2 (in Table 1) with a two-sided 5% significance level and 80% power gives the estimated number of subjects per group as 267.
Method 1 has given us a slightly smaller sample size estimate than Method 2. The two methods can be regarded as equivalent when the two populations are Normally distributed, with equal variances. In this case, the MW test will require about 5% more observations than the two-sample t-test to provide the same power against the same alternative. For non-Normal populations, especially those with long tails, the MW test may not require as many observations as the two-sample t-test [23].
Empirically, calculating a parametric estimate of Pr(Y > X) from the observed effect size data (using the observed sample means and standard deviations), leads to values very similar to the non-parametric estimate. For example, for the GH dimension in the CPSW data in Table 2, the observed non-parametric estimate of Pr(Y > X) was 0.542 compared to a parametric estimate of 0.537.
Sample size estimation – Method 3
Assuming a mean difference of 5 (i.e.

) and a common standard deviation of 20 (i.e.  ) for the GH dimension of the SF-36, then equation (1) leads to a parametric estimate of the effect size pNoether = Pr(Y > X) of 0.57. This in turn leads to a parametric estimate of the ARR (from equation 2), λ' = 0.57 - 0.43 = 0.14 and an estimated (from 3) OR θ' = 0.57/0.43 = 1.33.
) for the GH dimension of the SF-36, then equation (1) leads to a parametric estimate of the effect size pNoether = Pr(Y > X) of 0.57. This in turn leads to a parametric estimate of the ARR (from equation 2), λ' = 0.57 - 0.43 = 0.14 and an estimated (from 3) OR θ' = 0.57/0.43 = 1.33.
If we assume OROrdinal = OR = 1.33 then the assumption of proportional odds specifies that the OROrdinali will be the same for all 34 categories of the GH dimension. If we also assume the proportion of subjects in each category in the control group is the same as in Figure 1g. Then under the assumption of proportional odds OROrdinal = 1.33, the anticipated cumulative proportions (γ iT) for each category of treatment T are given by:

After calculating the cumulative proportions (γ
iT), the anticipated proportions falling into each treatment category, π
iT
can be determined from the difference in successive γ
iT. Finally, the combined mean ( ) of the proportions of treatments C and T for each category is calculated.
) of the proportions of treatments C and T for each category is calculated.
Substituting OROrdinal = 1.33 and  = 0.0067 with a two-sided 5% significance level and 80% power gives the estimated number of subjects per group as 584. Given this sample size, and with the distribution shown in Figure 1g and an OR of 1.33, we can work out what the corresponding mean values are. The estimated mean GH score was 77.6 in the treatment group and 75.0 in the control group. This is an estimated mean difference of 2.6 points, which is smaller than the five-point mean difference used earlier.
= 0.0067 with a two-sided 5% significance level and 80% power gives the estimated number of subjects per group as 584. Given this sample size, and with the distribution shown in Figure 1g and an OR of 1.33, we can work out what the corresponding mean values are. The estimated mean GH score was 77.6 in the treatment group and 75.0 in the control group. This is an estimated mean difference of 2.6 points, which is smaller than the five-point mean difference used earlier.
It is difficult to translate a shift in means into the shift in the probabilities on an ordinal scale, without several assumptions. If we assume proportions in each category in the control group as shown in Figure 1g and proportional odds shift, then an OROrdinal of 1.63 is approximately equal to a mean shift of 5.0. This leads to  = 0.007 and a sample size estimate of 199 subjects per group with two-sided 5% significance and 80% power. Given this sample size then the corresponding estimated mean GH scores are 74.8 and 79.8 in the control and treatment groups respectively.
= 0.007 and a sample size estimate of 199 subjects per group with two-sided 5% significance and 80% power. Given this sample size then the corresponding estimated mean GH scores are 74.8 and 79.8 in the control and treatment groups respectively.
Method 4 – Bootstrap sample size estimation
Figure 1g shows the skewed distribution of the GH dimension and that the underlying assumption of Normality of the distribution required for Method 1 may not be appropriate. Furthermore the, GH dimension is bounded by 0 and 100. Thus, if a new mother already has a GH score of 100 in the control group, then under the intervention no extra improvement can be seen, at least not by the GH dimension of the SF-36. Seven percent of women (35/487) in the Sheffield data had a GH score of 100 and 14.2% (70/487) had a score of 95 or more.
Figure 2 shows the estimated power curves for Methods 1, 2 and 3 and the two bootstrap methods (t and MW tests) at the 5% two-sided significance level for detecting a location shift (mean difference) δ = 5 in the SF-36 GH dimension using the data from the general population as our pilot sample, for sample sizes per group varying from 50 to 600. For these general population data a location shift of δ = 5 is equivalent to a standardised effect size Δ Normal = 0.25 and pNoether = Pr(Y > X) = 0.57. The bootstrap methods taking into account the bounded and non-Normal distribution of the data suggest a mean difference d of 4.5 and p = Pr(Y > X) = 0.58.
Estimated power curves for the SF-36 General Health dimension using general population data (females aged 16–45), based on α = 0.05 (two-sided) with 10,000 bootstrap replications SF-36 General Health Dimension (General Population Females aged 16–45); n= 487; mean = 74.8; sd = 19.6; 14.2% scoring 95 or more.
The GH dimension (Figure 1g) of the SF-36 has a large number (> 30) of discrete values or categories, most of which are occupied, and the proportion scoring 0 or 100 is low. Figure 2 suggests that the MW test is more powerful than the t-test for the GH dimension based on the bootstrap results for the bounded shift. The power curves shown in Figure 2 do not diverge too greatly and thus, the location shift hypothesis is a useful working model.
In contrast, Figure 3 shows the estimated power curves for another dimension of the SF-36: RP, which can only take one of five discrete values (as shown in Figure 1c), for detecting a simple location shift (mean difference) δ = 5. For these data a simple location shift of δ = 5 is equivalent to a standardised effect size Δ Normal = 0.17 and pNoether = Pr(Y > X) = 0.55. Since three-quarters of the pilot sample scored 100, the bootstrap methods under the location shift model, taking into account the bounded and non-Normal distribution of the data suggest a mean difference d of 1.2 and p = Pr(Y > X) = 0.51. The power curves shown in Figure 3 diverge greatly and the simple location shift hypothesis may not be appropriate for this outcome. Figure 3 clearly shows the value of the bootstrap in investigating the impact of the bounded HRQoL distributions on the power of the hypothesis test.
Estimated power curves for the SF-36 Role Physical dimension using general population data (females aged 16–45), based on α = 0.05 (two-sided) with 10,000 bootstrap replications SF-36 Role Limitations Physical Dimension (General Population Females aged 16–45); n= 487; mean = 85.5; sd = 29.1; 75.4% scoring 100.
Finally, Figure 4 shows the estimated power curves for the Vitality dimension of the SF-36. This computer simulation suggests that if the distribution of the HRQoL dimension are reasonably symmetric (Figure 1b), and the proportion of patients at each bound is low, then under the location shift alternative hypothesis, the t-test appears to be slightly more powerful than the MW test at detecting differences in means.
Use of the bootstrap to estimate Type I error
The bootstrap methodology provides an ideal opportunity to consider Type I errors. Resampling Algorithm 1 can easily be adapted for this. It simply involves modification of step 1 and not adding δ to the second simulated sample of patients. Under the true null hypothesis of no difference in distributions, the actual Type I error rate can be computed by determining the proportion of simulated cases which had significance levels at or below its nominal value. For a nominal Type I error rate of α = 0.05, we would expect 5% (or 0.05) of the bootstrap samples to give a (false-positive) significant result under the true null hypothesis of no difference in distributions. The robustness of each test can then be determining by comparing the actual Type I error rates to the nominal Type I error rates.
Statistical tests are said to be robust if the observed Type I error rates are close to the pre-selected or nominal, Type I error rates in the presence of violations of assumptions [24, 25]. Sullivan and D'Agostino [26] describe a test as 'robust' if the actual significance level does not exceed 10% of the nominal significance level (e.g. less than or equal to 0.055 when the nominal significance level is 0.05). They describe a test as 'liberal' if the observed significance exceeds the nominal level by more than 10%. Finally, they describe a test as 'conservative' if the actual significance level is less than the nominal level. A 'conservative' test is of less concern, as the probability of making a Type I error is controlled.
The overall actual significance levels relative to a nominal level of 0.05 under the null hypothesis of no treatment differences for the GH and RP dimensions are displayed in Table 3 for a variety of sample sizes. Both tests (t-test and MW) are 'robust' tests of the equality of means (and distributions) for both the GH and RP outcomes.
Extensions of the use bootstrap – odds ratio shifts rather than simple location shift
When using the proportional odds model to estimate sample size, Whitehead [16] and Julious et al [27] have pointed out that there is little increase in power (and hence saving in the number of subjects recruited) to be gained by increasing the number of categories in a proportional odds model beyond five. Although the model is robust to mild departures from the assumption of proportional odds, with increasing numbers of categories it is less likely that the proportional odds assumption remains true. Therefore, to illustrate this point, we shall use the five discrete category outcome of the RP dimension of the SF-36 to show the effect of the bootstrap sample size estimator when the alternative to the null hypothesis is an odds ratio transformation rather than a simple location shift.
Figure 5 shows the power curves for t-test and MW test for the RP dimension of the SF-36 assuming the alternative hypothesis is a proportional odds shift in HRQoL of OROrdinal = 1.50. As one would expect, the bootstrap power curves in Figure 5 show that the MW test or the equivalent proportional odds model is more powerful than the t-test when the alternative hypothesis is an odds ratio shift, although the differences in power for a given sample size are small.
Estimated power curves for the SF-36 Role Physical dimension to detect an Odds Ratio shift using general population data (females aged 16–45) based on α = 0.05 (two-sided) with 10,000 bootstrap replications Five category SF-36 Role Physical outcome (General population Females aged 16–45); n = 487, γ = (.06, .11, .17, .25, 1.0)
Sample sizes of over 450 patients per group are required to have an 80% chance of detecting this 'small to moderate' odds ratio (OR = 1.5) effect as statistically significant at the 5% two-sided level. With such 'large' sample sizes statistical theory, via Central Limit Theorem (CLT), guarantees that the sample means will be approximately Normally distributed, which ensures the relatively good performance of the t-test in detecting an OR location shift. The robustness of the two independent samples t-test when applied to three-, four- and five-point ordinal scaled data has previously been demonstrated by Heeren and D'Agostino [25] for far smaller sample sizes than this (as small as 20 per group).
Discussion
Choice of sample size method with HRQoL outcomes
It is important to make maximum use of the information available from other related studies or extrapolation from other unrelated studies. The more precise the information the better we can design the trial. We would recommend that researchers planning a study with HRQoL measures as the primary outcome pay careful attention to any evidence on the validity and frequency distribution of the HRQoL measures and its dimensions.
The frequency distribution of HRQoL dimension scores from previous studies should be assessed to see what methods should be used for sample size calculations and analysis. If the HRQoL outcome has a limited number of discrete values (say less than seven categories e.g. RP and RE dimensions, in the case of the SF-36, Figures 1c and 1f) and/or the proportion of cases at the upper bound (i.e. scoring 100) is high (e.g. PF, SF and BP dimensions in our general population sample example dataset, Figures 1a,1e,1f), then we would recommend using Method 3 to estimate the required sample size (Figure 6) [16]. In this case, the alternative hypothesis of a location shift model is questionable and the proportional odds model will provide a suitable alternative with such bounded discrete outcomes.
If the HRQoL outcome has a larger number of discrete values (greater than or equal to seven categories say), most of which are occupied and the proportion of cases at the upper or bounds (i.e. scoring 0 or 100, in the case of the SF-36) is low (e.g. VT, GH and MH dimensions in our general population sample example dataset, Figures 1b,1g and 1h), then the simple location shift model is a useful working hypothesis. We would therefore recommend using Methods (1) or (2) to estimate the required sample size (Figure 6).
Computer simulation has suggested that if the distributions of the HRQoL dimensions are reasonably symmetric (Figure 1b), and the proportion of patients at each bound is low, then under the location shift alternative hypothesis, the t-test appears to be slightly more powerful than the MW test at detecting differences in means (Figure 4). Therefore, if the distribution of the HRQoL outcomes is symmetric or expected to be reasonably symmetric and the proportion of patients at the upper or lower bounds is low then Method 1 could be used for sample size calculations and analysis (Figure 6). The use of parametric methods for analysis (i.e. t-test) also enables the relatively easy estimation of confidence intervals, which is regarded as good statistical practice [1].
If the distribution of the HRQoL outcome is expected to be skewed then the MW test appears to be more powerful at detecting a location shift (difference in means) than the t-test (Figures 2 and 3). Therefore, in these circumstances, the MW test is preferable to the t-test and Method 2 could be used for sample size calculations and analysis. However, using Method 2 for sample size estimation requires the effect size to be defined in terms of Pr(Y > X), which is difficult to quantify and interpret. Pragmatically we would recommend Method 1 as the effect size Δ Normal is rather easier to quantify and interpret than the effect size pNoether required for sample size estimation using Method 2 (Figure 6).
If the HRQoL data have a symmetric distribution, the mean and median will tend to coincide so either measure is a suitable summary measure of location. If the HRQoL data have an asymmetric distribution, then conventional statistical advice would suggest that the median is the preferred summary statistic [1]. However, a case when the mean and mean difference might be preferred (even for skewed outcome data) as a summary measure is when heath care providers are deciding whether to offer a new treatment or not to its population. The mean (along with the sample size) provides information about the total benefit (and total cost) from treating all patients, which is needed as the basis for health care policy decisions [28]. We cannot estimate the total benefit (or cost) from the sample median.
If the sample size is "sufficiently large" then statistical theory, using the CLT, guarantees that the sample means will be approximately Normally distributed. Thus, if the investigator is planning a large study and the sample mean is an appropriate summary measure of the HRQoL outcome, then pragmatically there is no need to worry about the distribution of the HRQoL outcome and we can use conventional methods to calculate sample sizes. Although the Normal distribution is strictly only the limiting form of the sampling distribution of the sample mean as the sample size n increases to infinity, it provides a remarkably good approximation to the sampling distribution even when n is small and the distribution of the data is far from Normal. Generally, if n is greater than 25, these approximations will be good. However, if the underlying distribution is symmetric, unimodal and continuous a value of n as small as 4 can yield a very adequate approximation [29]. If a reliable pilot or historical dataset of HRQoL data is readily available (to estimate the shape of the distribution) then bootstrap simulation (Method 4) will provide a more accurate and reliable sample size estimate than Methods 1 to 3 (Figure 6) [30].
We had a reliable historical data set of over 400 subjects so we had a large sample to estimate the distributions (cdfs) Fx and Fy under the null and alternative hypotheses using Method 4. Lesaffre et al [31] show that bootstrap can give fairly unbiased estimates of power, though for small pilot samples with large variability. In the absence of a reliable pilot set, bootstrapping is not appropriate and we will need to use conventional methods of sample size estimation or simulation models [32]. Fortunately, with the increasing use of HRQoL outcomes in research, historical datasets are becoming more readily available. White and Thompson [33] suggest the estimation of  (and hence
(and hence 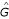 ) should be derived from a pilot dataset, and that the use of baseline data or related data sets (which we have used) is somewhat less satisfactory. They suggest a third possibility for estimating
) should be derived from a pilot dataset, and that the use of baseline data or related data sets (which we have used) is somewhat less satisfactory. They suggest a third possibility for estimating  is to use follow-up data viewed in a blinded manner, although only when the blinding can demonstrably be preserved.
is to use follow-up data viewed in a blinded manner, although only when the blinding can demonstrably be preserved.
Strictly speaking, our results and conclusions only apply to the SF-36 outcome measure. Further empirical work is required to see whether or not these results hold true for other HRQoL outcomes, populations and interventions. However, the SF-36 has many features in common with other HRQoL outcomes, such as the NHP and QLQ-C30, i.e. multi-dimensional, ordinal or discrete response categories with upper and lower bounds, and skewed distributions; therefore, we see no theoretical reason why these results and conclusions with the SF-36 may not be appropriate for other HRQoL measures.
Throughout this paper, we only considered the situation where a single dimension of HRQoL is used at a single endpoint. We have assumed a rather simple form of the alternative hypothesis that the new treatment/intervention would improve HRQoL compared to the control/standard therapy. This form of hypothesis (superiority vs. equivalence) may be more complicated than actually presented. However, the assumption of a simple form of the alternative hypothesis that new treatment/intervention would improve HRQoL compared to the control/standard therapy, is not unrealistic for most superiority trials and is frequently used for other clinical outcomes.
We have based the calculations above on the assumption that there is a single identifiable endpoint, or HRQoL outcome, upon which treatment comparisons are based (in our case the GH dimension of the SF-36). Sometimes there is more than one endpoint of interest; HRQoL outcomes are multi-dimensional (e.g. the SF-36 has eight dimensions including GH). If one of these dimensions is regarded as more important than the others, it can be named as the primary endpoint and the sample size estimates calculated accordingly. The remainder should be consigned to exploratory analyses or descriptions only [3]. Fairclough gives a more comprehensive discussion of multiple endpoints and suggests several methods for analysing HRQoL outcomes [34].
More work is required on what is a clinically meaningful effect sizes for the SF-36 and other HRQoL outcomes. There is an extensive literature on the important issue of clinically meaningful change and the minimum important difference (MID) for HRQoL outcomes. As the subject of this paper is the use of computer intensive methods such as the bootstrap we have played down the issue of the MID. Again for brevity and practical purposes of sample size estimation this paper has assumed the MID for the SF-36 outcome is around five points for each dimension. This is an important issue in sample size estimation. The interested reader is referred to a series of papers from the Clinical Significance Consensus Meeting Group for more detailed discussion [35].
Conclusion
Finally, we would stress the importance of a sample size calculation (with all its attendant assumptions), and that any such estimate is better than no sample size calculation at all, particularly in a trial protocol [36]. The mere fact of calculation of a sample size means that a number of fundamental issues have been thought about: what is the main outcome variable, what is a clinically important effect, and how is it measured? The investigator is also likely to have specified the method and frequency of data analysis. Thus, protocols that are explicit about sample size are easier to evaluate in terms of scientific quality and the likelihood of achieving objectives.
References
Altman DG, Machin D, Bryant TN, Gardner MJ: Statistics with Confidence: Confidence intervals and statistical guidelines 2 Edition London: British Medical Journal 2000.
Machin D, Campbell MJ, Fayers PM, Pinol APY: Sample Sizes Tables for Clinical Studies 2 Edition Oxford: Blackwell Science 1997.
Fayers PM, Machin D: Quality of Life Assessment, Analysis and Interpretation Chichester: Wiley 2000.
Walters SJ, Campbell MJ, Lall R: Design and Analysis of Trials with Quality of Life as an Outcome: a practical guide. Journal of Biopharmaceutical Statistics 2001,11(3):155–176. 10.1081/BIP-100107655
Walters SJ, Campbell MJ, Paisley S: Methods for determining sample sizes for studies involving health-related quality of life measures: a tutorial. Health Services & Outcomes Research Methodology 2001, 2: 83–99. 10.1023/A:1020102612073
Efron B, Tibshirani RJ: An Introduction to the Bootstrap New York: Chapman & Hall 1993.
Morrell CJ, Spiby H, Stewart P, Walters S, Morgan A: Costs and effectiveness of community postnatal support workers: randomised controlled trial. British Medical Journal 2000, 321: 593–598. 10.1136/bmj.321.7261.593
Staquet MJ, Hays RD, Fayers PM: Quality of Life Assessment in Clinical Trials: Methods and Practice Oxford: Oxford University Press 1998.
Ware JE Jr, Sherbourne CD: The MOS 36-item short-form health survey (SF-36). I. Conceptual framework and item selection. Medical Care 1992, 30: 473–483.
Brazier JE, Harper R, Jones NMB, O'Cathain A, Thomas KJ, Usherwood T, Westlake L: Validating the SF-36 health survey questionnaire: new outcome measure for primary care. British Medical Journal 1992, 305: 160–164.
Pocock SJ: Clinical Trials: A Practical Approach Chichester: Wiley 1983.
Lehman EL: Nonparametric Statistical Methods Based on Ranks San Francisco: Holden-Day 1975.
Noether GE: Sample Size Determination for Some Common Nonparametric Tests. J American Statistical Association 1987,82(398):645–647.
Hamilton MA, Collings BJ: Determining the Appropriate Sample Size for Nonparametric Tests for Location Shift. Technometrics 1991,3(33):327–337.
Simonoff JS, Hochberg Y, Reiser B: Alternative Estimation Procedures for Pr(X < Y) in Categorised Data. Biometrics 1986, 42: 895–907.
Whitehead J: Sample size calculations for ordered categorical data. Statistics in Medicine 1993, 12: 2257–2271. [published erratum appears in Stat Med 1994 Apr 30;13(8):871].
Campbell MJ: Statistics at Square Two: Understanding Modern Statistical Applications in Medicine London: British Medical Journal 2001.
Shepstone L: Re-conceptualising and Generalising the Absolute Risk Difference: A unification of Effect Sizes, Odds Ratios and Number-Needed-to-Treat. Journal of Epidemiology & Community Health 2001,55((Suppl 1) 1a):A7.
Collings BJ, Hamilton MA: Estimating the Power of the Two-Sample Wilcoxon Test for Location Shift. Biometrics 1998, 44: 847–860.
Walters SJ, Brazier JE: Sample Sizes for the SF-6D Preference Based Measure of Health from the SF-36: A Comparison of Two Methods. Health Services & Outcomes Research Methodology 2003, 4: 35–47. 10.1023/A:1025876827228
Simon JL: Resampling Stats: Users Guide. v5.02 Arlington: Resampling Stats Inc 2000.
Ware JE Jr, Snow KK, Kosinski M, Gandek B: SF-36 Health Survey Manual and Interpretation Guide Boston, MA The Health Institute, New England Medical Centre 1993.
Elashoff JD: nQuery Advisor Version 3.0 User's Guide Los Angeles Statistical Solutions 1999.
Sullivan lM, D'Agostino RB: Robustness and power of analysis of covariance applied to data distorted from Normality by floor effects. Statistics in Medicine 1996, 15: 477–496. Publisher Full Text 10.1002/(SICI)1097-0258(19960315)15:5<477::AID-SIM217>3.0.CO;2-R
Heeren T, D'Agostino RB: Robustness of the two independent samples t -test when applied to ordinal scaled data. Statistics in Medicine 1987, 6: 79–90.
Sullivan lM, D'Agostino RB: Robustness and power of analysis of covariance applied to ordinal scaled data as arising in randomized controlled trials. Statistics in Medicine 2003, 22: 1317–1334. 10.1002/sim.1433
Julious SA, George S, Machin D, Stephens RJ: Sample sizes for randomized trials measuring quality of life in cancer patients. Quality of Life Research 1997, 6: 109–117. 10.1023/A:1026481815304
Thompson SG, Barber JA: How should cost data in pragmatic randomised trials be analysed? British Medical Journal 2000, 320: 1197–1200. 10.1136/bmj.320.7243.1197
Hogg RV, Tanis EA: Probability and Statistical Inference 3 Edition New York: McMillan 1988.
Troendle JF: Approximating the Power of Wilcoxon's Rank-Sum Test Against Shift Alternatives. Statistics in Medicine 1999, 18: 2763–2773. 10.1002/(SICI)1097-0258(19991030)18:20<2763::AID-SIM197>3.3.CO;2-D
Lesaffre E, Scheys I, Frohlich J, Bluhmki E: Calculation of power and sample size with bounded outcome scores. Statistics in Medicine 1993, 12: 1063–1078.
Tsodikov A, Hasenclever D, Loeffler M: Regression with Bounded Outcome Score: Evaluation of Power by Bootstrap and Simulation in a Chronic Myelogenous Leukaemia Clinical Trial. Statistics in Medicine 1998, 17: 1909–1922. 10.1002/(SICI)1097-0258(19980915)17:17<1909::AID-SIM890>3.0.CO;2-0
White IR, Thomson SG: Choice of test for comparing two groups, with particular application to skewed outcomes. Statistics in Medicine 2003, 22: 1205–1215. 10.1002/sim.1420
Fairclough DL: Design and Analysis of Quality of Life Studies in Clinical Trials New York: Chapman & Hall 2002.
Cella D, Bullinger M, Scott C, Barofsky I, and the Clinical Significance Consensus Meeting Group: Group vs individual approaches to understanding the clinical significance of differences or changes in quality of life. Mayo Clinic Proceedings 2002,77(4):384–392.
Williamson P, Hutton JL, Bliss J, Blunt J, Campbell MJ, Nicholson R: Statistical review by research ethics committees. J Roy Statist Soc A 2000, 163: 5–13. 10.1111/1467-985X.00152
Author information
Authors and Affiliations
Corresponding author
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
About this article
Cite this article
Walters, S.J. Sample size and power estimation for studies with health related quality of life outcomes: a comparison of four methods using the SF-36. Health Qual Life Outcomes 2, 26 (2004). https://doi.org/10.1186/1477-7525-2-26
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1477-7525-2-26





